Средняя квадратическая погрешность

Погрешность При Межевании Земельных Участков 2020

Тенденция того, что одна ошибка может в будущем привести к трем другим, в рамках современного землеустроения стала нормой, одновременно спровоцировав психоз среди населения, когда землевладелец утратил уверенность в законности своего права и вообще в том, что имеющийся участок действительно принадлежит ему.

Рекомендуем прочесть: Норматив потребления воды на 1 человека без счетчика с 2020 ульяновск

Итогом ее является документальное и практическое определение формы участка, его границ и положения на местности. Ошибки в ходе данных работ и являют собой причинно-следственные основы будущих споров, а подчас и плачевных правовых последствий для потенциального собственника. Так, в методиках проведения межевания и земельном законодательстве присутствует такой термин, как допустимая погрешность.

Пример вычисления стандартного отклонения оценок учеников

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

2 , 4 , 4 , 4 , 5 , 5 , 7 , 9.

Тогда средняя оценка равна:

μ = 2 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 >=5>

Вычислим квадраты отклонений оценок учеников от их средней оценки:

( 2 − 5 ) 2 = ( − 3 ) 2 = 9 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 7 − 5 ) 2 = 2 2 = 4 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 9 − 5 ) 2 = 4 2 = 16 (2-5)^=(-3)^=9&&(5-5)^=0^=0\\(4-5)^=(-1)^=1&&(5-5)^=0^=0\\(4-5)^=(-1)^=1&&(7-5)^=2^=4\\(4-5)^=(-1)^=1&&(9-5)^=4^=16\\\end>>

Среднее арифметическое этих значений называется дисперсией:

σ 2 = 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 8 = 4 =>=4>

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

σ 2 = 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 7 ≈ 4 , 57 =>\approx 4,57>

и стандартное отклонение равнялось бы:

σ = 4 , 57 ≈ 2 , 14 >\approx 2,14>

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Источник

Расчет точности геодезических работ

Для выполнения работ использовался тахеометр TCR405Power. Электронный тахеометр Leica TCR 405 Power имеет следующие параметры СКО измерения расстояний:

СКО изм.расст. = 2 мм + 2 ppm

Ppm- Миллионная доля — единица измерения каких-либо относительных величин, равная 1·10−6 от базового показателя

СКО изм.расст. = 2+(2*D(км)^ 10−6)мм

где D-расстояние от прибора до измеряемого объекта

Рассмотрим приведенные выше формулы и характеристики оборудования применительно к данному объекту. Изучим точность геодезических работ на объекте.

Проанализировав расстояния, минимальное 30м и максимальное 303м, подставив значения в формулы, смотрим погрешности.

Погрешность измерения расстояний на нашем объекте рассчитаем по выше приведенной формуле: 1. СКО изм.расст. = 2+(2*D(км)^ 10−6)мм

2. СКО изм.расст. = 2+(2*0,303(км)^ 10−6)мм = 2,000мм

3. СКО не превышает заявленных паспортных значений для нашего оборудования.

Для расчета среднеквадратической ошибки угловых измерений применялась следующая формула Гаусса и Бесселя:

где ∆ – СКО геодезического прибора, n – количество приемов.

М=√5″^2/3=2.89″

Исходя из выше полученных результатов СКО расстояний и углов, рассчитаем значение возможной ошибки превышений.

Превышения вычисляются по следующей формуле:

h = d*tgᶹ

где, D это расстояние в м, а α-угол измерения в ⁰.

Высота инструмента и высота вехи при вычислении СКО не учитывается. Так как оценивается только точность измерений превышения. Высота вехи статична и одинакова на протяжении всего цикла и может не учитываться, а высотная отметка точки стоянии прибора не важна.

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Понятие о неравноточных измерениях

_______ Неравноточными измерениями называются такие, которые выполнены различным числом приемов, приборами различной точности и т.д. Если измерения неодинаковой точности, то для определения общей арифметической середины пользуются формулой:

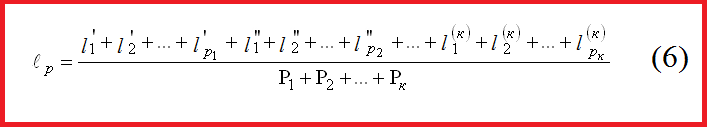________ Весом называется число, которое выражает степень доверия к результату измерения. В тех случаях, когда неизвестны веса измеренных величин, а известны их средние квадратические ошибки, то веса можно вычислить по формуле:

т.е. вес результата измерений обратно пропорционален квадрату средней квадратической ошибки.

_______ При неравноточных измерениях средняя квадратическая ошибка измерения, вес которого равен единице, определяется по формуле:

где δ – разность между отдельными результатами измерений и общей арифметической серединой.

Источник

Оценка точности измерений

_______ Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:

_______ 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической середины х = /n. _______ 2. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: = 0; _______ 3. По формуле вычисляют среднюю квадратическую ошибку одного измерения. _______ 4. По формуле вычисляют среднюю квадратическую ошибку арифметической средины. _______ 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.

_______ 6. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.

Случайные и систематичес­кие погрешности

Погрешности подразделяются на случайные и систематичес­кие. Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить. Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины. Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.

Классификация ошибок измерений

_______ Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

_______ При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые , систематические и случайные .

_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

_______ Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

_______ Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений _______

_______ В основу теории ошибок положены следующие свойства случайных ошибок : _______ 1. Малые ошибки встречаются чаще, а большие реже. _______ 2. Ошибки не превышают известного предела. _______ 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются. _______ 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.

_______ По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

_______ Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами.

_______ Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

Что делать, если граница спорная

Межевание довольно часто происходит между соседями по земельным наделам, и возникают некоторые накладки. Например, неизбежные ошибки и соответствующие споры. Так, граница может быть уже занесена в кадастр, а на местности у собственника и соседа (например, если собственник новый) возникли вопросы относительно ее точности и происхождения.

В этом случае нужно выяснить через соответствующие инстанции, с какой именно погрешностью была установлена граница. Более сложный вариант — вызов кадастрового инженера и инициация процедуры по выносу границ в натуру, а также прибегать к землеустроительной экспертизе. Это недешево, но туда входит не только выявление «виновника» возникшего спора, но и предоставление рекомендуемых способов для устранения причины раздоров. Но эти варианты возможны только в том случае, если сосед готов к диалогу.

Если же в этом нет уверенности, но при межевании произошла ошибка, и границы смежных земель наложились друг на друга, площадь одного из участков сократилась, обращаются в Государственный Кадастр Недвижимости. Закон гласит, что такую ошибку исправлять нужно их сотрудникам. Если там решат, что ошибка была допущена несущественная, то вы получите отказ в исправлении.

Если у собственника участка, который урезали из-за ошибки, хорошие соседи, он должен попытаться добиться устранения недоразумения мирным путем, без суда. Достаточно обратиться к соседу и в ГНК с просьбой исправить допущенную ошибку, не доводя все до суда. Это срабатывает при двух условиях:

1. Сосед согласится провести новое межевание совместно, и это одна из множества причин, почему с соседями лучше всего быть в хороших отношениях.
2. ГНК все же согласится исправить ошибку.

Это необходимо сделать, если сосед на новое межевание не согласится. Необходимо зафиксировать этот факт письменно.

Итак, если таким путем решить вопрос не удалось, придется обращаться в суд. Обращение должно касаться двух моментов:

1. Общего с соседом проведения нового межевания, чтобы восстановить границы участка.
2. Исправления ошибки в записях кадастра.

Затем собирается необходимая документация, включая и письменное свидетельство о том, что дело пытались решить без участия суда. Нужно также взять заключение кадастрового инженера и выписку о существующих границах надела из кадастра. После этого документацию направляют в суд. Дело же истца — подобрать специалистов правильно.

Как определяются границы земельного участка?

Любой земельный участок в геодезии рассматривается в качестве плоской геометрической фигуры определённой формы, а границей считается совокупность всех линий, которые и составляют эту фигуру. Для определения фактической границы проводится геодезическое межевание. Сколько по времени делается межевание земельного участка узнайте тут. Во время межевания кадастровый инженер определяет географические координаты так называемых узловых точек, соединив которые прямыми линиями можно получить границы участка.

• Если участок имеет прямоугольную форму, а какие-либо дефекты рельефа отсутствуют, то в таком случае достаточно определить координаты вершин прямоугольника, которые и будут являться узловыми точками.
• Если же участок имеет вид сложной геометрической фигуры и/или имеются дефекты рельефа, то тогда вводятся дополнительные узловые точки, которые будут более точно определять границы.

Границы земельного участка могут определяться исключительно кадастровым инженером. Видео того, как делается межевание земельного участка прямо здесь.

В качестве такого работника могут выступать следующие лица:

1. Государственные инженеры, которые прошли соответствующую подготовку и числятся в штате соответствующей государственной организации.
2. Сотрудники частных организаций, у которых есть государственная лицензия на ведение подобной деятельности.
3. Частные инженеры-предприниматели, которые прошли подготовку и имеют государственную лицензию.

После межевания в Кадастровый реестр вносятся сведения о координатах узловых точек. Стоимость постановки земельного участка на кадастровый учёт в этой статье. Если у хозяина земли появились сомнения по поводу достоверности границ, то он может обратиться в Кадастровые органы для проведения повторного межевания, а в случае обнаружения кадастровых ошибок информация о координатах может быть пересмотрена. Мы уже написали подробно о том, можно ли изменить границы земельного участка после межевания в отдельной статье.

Межевание рекомендуется сделать в том случае, если оно ещё ни разу не проводилось, например, если участок вам достался по наследству, поскольку в противном случае имущественные права хозяина будут сильно ограничены. Эту территорию нельзя продать, сдать в аренду, подарить или завещать.

Возникла проблема? Позвоните юристу:

Москва и Московская область (звонок бесплатен) Санкт-Петербург и Лен.область

От чего зависит точность определения координат при межевании?

Точность определения координат зависит от следующих факторов:

1. Квалификация инженера и методика измерения. Для подсчёта результатов могут использоваться разные методики, каждая из которых имеет свою плюсы и минусы. Также нужно учитывать человеческий фактор, поскольку на практике встречаются ситуации, когда кадастровые ошибки появляются из-за недобросовестности инженеров-геодезистов.
2. Точность измерительных приборов. Сегодня для измерения координат применяются GPS-навигаторы, а также различные геодезические приборы для оценки формы рельефа. Некоторые приборы (например, старые навигаторы) несколько отстают от современных, что может привести к появлению ошибки.
3. Внешние факторы. На точность могут оказать влияния и некоторые другие факторы — неблагоприятные погодные условия, температура воздуха, неровность рельефа и так далее.

Результаты геодезических измерений

Под результатом геодезического измерения подразумевается конечный результат, который получается в процессе всех произведённых измерений и вычислений. Например, конечным результатом может быть высота точки, её плановые координаты, площадь участка и т.п.

Равноточные и неравноточные измерения

Результаты геодезических измерений в своей группе могут быть равноточными и неравноточными.

Если измерения выполнены прибором одного и того же класса точности, по одной и той же методике (программе), в одинаковых внешних условиях, одним и тем же наблюдателем (либо наблюдателями одной квалификации), то такие измерения относят к равноточным. При несоблюдении хотя бы одного из перечисленных выше условий результаты измерений классифицируют как неравноточные.

Примером равноточных измерений могут являться результаты измерений длины одной и той же линии либо линий, примерно равных друг другу, полученные при неизменных условиях внешней среды, одним и тем же измерительным средством (прибором), одними и теми же исполнителями работ, по общей для всех результатов измерений программе.

Если в процессе измерений длины линии, например, светодальномером, изменится температура окружающего воздуха, влажность, давление, то это может привести к получению части неравноточных результатов в общей группе результатов измерений, поскольку при изменении внешних условий может произойти и изменение характеристик измерительного прибора, характеристик прохождения светового луча в атмосфере.

Необходимые и избыточные числа измеренных величин и измерений

Число измеренных величин и число измерений может быть необходимым и избыточным.

При измерении, например, углов в треугольнике число необходимых измеренных величин равно двум, в семиугольнике – шести. Значение третьего (седьмого) угла можно вычислить по сумме двух (шести) измеренных углов. Если необходимо решить плоский треугольник, то дополнительно к измеренным двум углам обязательным является знание длины хотя бы одной из его сторон, в связи с чем число необходимых измеренных величин должно быть равно трём (одно измерение – линейное, два – угловые). Та же задача решается и при выполнении двух линейных измерений и одного угла, заключённого между измеренными сторонами треугольника.

Таким образом, числом необходимых измеренных величин является минимально необходимое их число, при котором обеспечивается решение поставленной задачи. Число же измеренных величин, превышающих число необходимых, называется числом избыточных величин. В геодезии, в маркшейдерии принято, но и не только принято, а является обязательным, получать и избыточные величины, что обеспечивает обнаружение грубых погрешностей и промахов, позволяет повысить точность результатов измерений. Поэтому в треугольнике, например, обязательно измеряют все три угла и сравнивают полученную сумму углов с теоретической.

Если сформулировать задачу с точки обеспечения заданной точности измерений, то необходимое число измерений должно обеспечивать заданную точность измерения одной величины или самого результата измерений. Так, в том же треугольнике, каждый из его углов может быть измерен несколько раз. Все избыточные измерения повышают надёжность результатов, а также их точность, но в то же время и увеличивают объём работ, и часто прирост увеличения точности становится экономически нецелесообразным из-за большого числа измерений. Иногда говорят, что числом необходимых измерений, например, горизонтального угла, является одно измерение, остальные – избыточные. Это не всегда так, поскольку, одно измерение не позволяет производить оценку точности и может содержать неконтролируемую грубую погрешность (промах).

Стандартное отклонение

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Характерные точки границ земельного участка

Для определения местоположения земельного участка ключевое значение имеет описание границ участка.

Под местоположением участка понимаются координаты характерных точек его границ, то есть точек изменения описания границ участка и деления их на части (пункт 7 статьи 38 Федерального закона от 24 июля 2007 года № 221-ФЗ «О государственном кадастре недвижимости»). Данный закон утрачивает свою силу с 01 января 2020 года, однако аналогичное определение содержится в новом Федеральном законе от 13 июля 2020 года № 218-ФЗ «О государственной регистрации недвижимости».

В отношении отдельных частей границ нормативными актами может предусматриваться иная процедура определения их местонахождения: путем указания на природные или искусственно возведенные объекты, сведения о которых имеются в Государственном кадастре недвижимости и чьи границы совпадают с внешними границами участка.

Процедура, способы и методы определения координат характерных точек границ земельного участка регламентируются Приказом Министерства экономического развития РФ от 17 августа 2012 года № 518.

Основой для установления характерных границ является система координат, установленная законодательством для ведения государственного кадастра недвижимости (ГКН). Для практического определения координат характерных точек используются следующие методы:

• 1) Геодезический метод;
• 2) Метод спутникового геодезического измерения;
• 3) Фотограмметрический метод;
• 4) Картометрический метод;
• 5) Аналитический метод.

Размах вариации

Вариация — это различия значений признака у единиц исследуемой совокупности. Она образуется из-за того, что индивидуальные значения формируются при различных условиях. Выборка должна быть представительной, чтобы по результатам её исследований можно было сделать правильные выводы о характеристиках всей совокупности.

Количественная репрезентативность достигается при использовании достаточного числа наблюдений в выборке, которое может обеспечить получение достоверных результатов. Качественная репрезентативность заключается в одинаковой структуре выборочной и генеральной совокупностей по признакам, имеющим влияние на получение конечного результата. К абсолютным показателям вариации относятся:

• размах, R;
• среднее линейное отклонение, a;
• среднеквадратичное отклонение, σ (сигма);
• дисперсия, D.

Размах вариации показывает абсолютную разницу между максимумом и минимумом значений признака:

R = x max — x min, где x — значения признака.

Интерпретация величины среднеквадратического отклонения

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: , и . У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины

Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить

Законодательство

Межевание земельных наделов регулируется законом. Он же устанавливает, какую по величине разрешено допускать ошибку. 13 часть статьи 22 закона № 218 говорит о том, что все погрешности измерения координат ключевых точек и методы, которыми производят замеры, а также формулы расчета отображены в приказе № 90 Минэкономразвития.

Законодательно являются разрешенными такие методы:

• спутниковый;
• аналитический;
• картометрический;
• фотографический;
• полигонометрический.

Также все технические тонкости регулируются и письмами Минэкономразвития № 518 и № 582.

Все необходимые операции и все то, что нужно для их выполнения, закреплено юридически, а не просто прихоти землемера или организации, чьими услугами было решено воспользоваться.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ = D >>

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Источник

Оценка точности измерений

_______ Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:

_______ 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической середины х = /n. _______ 2. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: = 0; _______ 3. По формуле вычисляют среднюю квадратическую ошибку одного измерения. _______ 4. По формуле вычисляют среднюю квадратическую ошибку арифметической средины. _______ 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.

_______ 6. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.

Погрешности по характеру действий

По данному признаку все ошибки можно разделить на следующие отклонения:

• грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
• систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
• случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;

Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.

Определение погрешности измерений геодезия

Погрешности геодезических измерений

Погрешность геодезических измерений (ошибка результата геодезических измерений) — отклонение результата геодезических измерений от истинного (действительного) значения измеряемой геодезической величины.

В геодезии, астрономии, фотограмметрии, картографии традиционно применяется понятие «ошибка», а также понятие «невязка».

Случайная составляющая погрешности (геодезических) измерений Погрешность геодезических измерений: выраженная в единицах измеряемой геодези-ческой величины.

относительная погрешность (геодезических) измерений Параметр функции распределения результатов измерений, характеризующий их рас-сеяние и равный положительному значению корня квадратного из дисперсии результата из-мерений. Примечание. 1. Дисперсия случайной величины равна математическому ожиданию квадратов отклонения случайной величины от ее математического ожидания: ?2 = M 2. 2. В геодезической практике среднее квадратическое отклонение вычисляется при исключении влияния систематических погрешностей измерений (при этом подразумевается отсутствие или предварительное исключение систематиче-ских погрешностей измерений).

Ссредняя квадратическая погрешность результата (геодезических) измерений; СКП Эмпирическая оценка среднего квадратического отклонения результата измерений. Примечание. Оценка m погрешности отдельного результата геодезических из-мерений может быть получена одним из следующих способов: • по отклонениям результатов измерений от среднего арифметического mvni=??21, где n — количество измерений, vi — отклонение отдельных измерений от их среднего арифметического; 10 • по отклонениям результатов измерений от истинного (эталонного) значения mni=??2, где ?i — отклонения отдельных результатов от истинного значения величины. n — количество измерений • по невязкам функций измеренных геодезических величин mwqni=?2, где wi- невязка функции измеренных величин; q — количество измеренных величин, участвующих в образовании невязки; n — количество невязок.

Предельная погрешность (геодезических) измерений Погрешность геодезических измерений, которую с заданной вероятностью не должны превышать по абсолютному значению погрешности результатов измерений.

Допустимая погрешность (геодезических) измерений Д>/предел допускаемой погрешности геодезических измерений / Погрешность геодезических измерений, верхний предел которой установлен в норма-тивной документации.

Источник