Определение площади объекта недвижимости

Предварительный просмотр:

Муниципальное автономное образовательное учреждение

«Средняя общеобразовательная школа № 7»

Научно-практическая конференция «Шаг в будущее»

«РАЗЛИЧНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ

Авторы : ученики 11 «И» класса

Дубица Ольга Сергеевна

Кондрашкина Алина Андреевна

Руководитель : учитель математики

Новолодская Лариса Владимировна

Великие математики о вычислении площадей ………………………….6

Георг Пик и его теорема ……………………………………………………7

Способы вычисления площадей многоугольников …………………….8

Первое условие, которое надлежит выполнять в математике, —

это быть точным, второе –

быть ясным и, насколько можно, простым. Лазар Карно

СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ

Процесс определения площади земельных участков или любых других объектов недвижимости включает следующие этапы:

1. Выполнение измерений при помощи различных технических средств;

2. Вычислительная обработка результатов измерений;

3. Составление экспликации по площадям угодий (сводные данные).

В зависимости от формы земельных участков и используемых технических средств применяют следующие способы определения площадей:

1. Аналитический – основан на вычислении площади по результатам измерений линий и углов на местности с применением формул геометрии и тригонометрии, а также по координатам вершин точек поворота границы земельного участка;

2. Графоаналитический – основан на вычислении площади по результатам измерений на плане. Участок разбивается на простейшие геометрические фигуры или измерения производятся при помощи палеток;

3. Механический – основан на измерении площадей на плане или карте при помощи планиметров.

Наиболее точен аналитический способ, так как здесь сказываются только ошибки измерений на местности. Он требует большого объёма вычислений. Хотя при наличии карт на цифровых носителях и современной вычислительной техники это не имеет особого значения.

Наиболее распространён благодаря скорости и простоте определения площадей на бумажных носителях механический способ. Хотя он менее точен.

Графический способ есть смысл применять, когда граница прямолинейна и имеет малое число поворотов, или площадь участка на плане менее 3 см. Для определения площади земельного участка, границы которого имеют прямолинейные очертания и большое число точек поворота, деление на треугольники нежелательно. Более предпочтительным вариантом является вычисление площади по координатам точек поворота границы землепользования. Координаты точек поворота графически снимаются при помощи циркуля-измерителя и определяются по линейке поперечного масштаба.

studopedia.ru

arbitrnw.ru

Бесплатная консультация по телефону Вся Россия » » » ООО ГУП «Комитет землеустройства и кадастра объектов недвижимости» ( www.komitet-zem.ru ), являясь лицом, обладавшим на день вступления в силу Федерального закона от 24.07.

2007 № 221-ФЗ «О государственном кадастре недвижимости» правом выполнения работ по территориальному землеустройству, считающимся кадастровым инженером в переходный период, до 1 января 2011 года имело право на выполнение кадастровых работ, в том числе кадастровых работ по уточнению местоположения границ земельных участков.

В соответствии с п. В программе реализован механизм подстановки значений в формулу расчета предельно допустимой погрешности определения площади и формулу для расчета средней квадратической погрешности положения характерных точек границ.

N 518 г. Москва «О требованиях к точности и методам определения координат характерных точек границ земельного участка, а также контура здания, сооружения или объекта незавершенного строительства на земельном участке»

Зарегистрирован в Минюсте РФ 25 декабря 2012 г. Регистрационный N 26340 В соответствии с частью 7 статьи 38 и частью 10 статьи 41 Федерального закона от 24 июля 2007 г.

N 221-ФЗ «О государственном кадастре недвижимости» (Собрание законодательства Российской Федерации, 2007, N 31, ст. 4017; 2008, N 30, ст. 3597; 2009, N 52, ст.

Врио Министра А. Клепач Приложение Требования к точности и методам определения координат характерных точек границ земельного участка, а также контура здания, сооружения или объекта незавершенного строительства на земельном участке 1.

Какая допускается погрешность при межевании земельных участков

Межевание земельных участков относится к важнейшим процедурам, необходимым для установления или подтверждения права собственности на землю с целью дальнейшего распоряжения ею. Специфика процедуры (геодезические инструменты, сложный рельеф местности и пр.) приводит к возникновению погрешности, допустимой по закону.

Для села, города, промышленной зоны и т.д. размер допустимой погрешности разный.

земельных участков позволяет закрепить юридическое право владения ЗУ.

Точные границы ЗУ определяются по с помощью принятых на момент геодезической съемки координат и проводятся с выносом на местность.

Результаты закрепляются в пакете технической документации.

Межевание земель: допустимая погрешность

› › Земельные вопросы в последние 3 года стали актуальнее.

Связать это можно с регулярными изменениями в земельном законодательстве, а также стартовавшим в июне сего года призывом произвести межевание да 2020 года.Основной причиной такого поведения со стороны властей стали участившиеся земельные споры, что привело к необходимости упорядочения и ревизии земельного фонда страны.

Так, по сути, сами граждане и спровоцировали такую ситуацию.

Споры и рассуждения на эту тему присутствовали всегда, но на текущем этапе земельных отношений достигли своей критической точки.

Тенденция того, что одна ошибка может в будущем привести к трем другим, в рамках современного землеустроения стала нормой, одновременно спровоцировав психоз среди населения, когда землевладелец утратил уверенность в законности своего права и вообще в том, что имеющийся участок действительно принадлежит ему.Виной всему пресловутый

Способы определения площади земельного участка

При проведении землеустроительных работ используются различные способы вычисления Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.

Полигон: межевой план

Если речь идет о расчете предельно допустимой погрешности при вычислении площади ЗУ, то основная формула такова: ∆Р*Mt*√P В данной формуле применяются следующие значения: Показатели Описание ∆Р (дельта Р) это разница между вычисленной площадью земельного участка (Р выч, выражается в кв. метрах)и площадью ЗУ, указанной в правоустанавливающем документе или документе, удостоверяющем право на конкретный участок земли (Рдок, выражается в кв. метрах)) Mt это средняя квадратическая ошибка положения межевого знака, то есть величина погрешности, применяемая земель той или иной категории (выражена в метрах) Р площадь ЗУ Данные из кадастровой выписки или правоустанавливающего документа сравниваются с данными геодезического замера, а полученную величину погрешности сравнивают с предельно допустимыми величинами согласно категории земли.

Необходимые документы

Для установления границ участка можно обратиться в любое кадастровое агентство либо кадастровый центр. Для оформление заказа на осуществление процедуры потребуется минимальный пакет документов:

• выписка из ЕГРН «Об объекте нежвижимости»;
• свидетельство, подтверждающее право собственности;
• кадастровый план территории;
• разрешение на проведение работ от лиц, проживающих по соседству (опционально);
• геодезические и картографические материалы.

Некоторые организации предлагают самостоятельно получить документы для заказчика, если какие-то из необходимых у него отсутствуют.

Процедура межевания должна производиться строго в соответствии с требованиями, предъявляемыми законом. Изучим эти требования в двух различных направлениях работ.

Определение координат межевых знаков

Производится с использованием ряда методов в т.ч. метод картографии, фотограмметрический метод, геодезические измерения через спутник, триангуляция, комбинированные засечки и лучевые системы.

В зависимости от выбранного метода определения специалист использует специальные инструменты. Это могут быть спутниковые приемники, теодолиты, фотограмметрические приборы, дигитайзеры и т.д.

Результатом проведенных работ становится определение координат пунктов ОМС и межевых знаков.

Определение площади участка

Площадь участков определяется с использованием графического, механического или аналитического способа. При необходимости эти способы могут сочетаться либо действовать по отдельности. В процессе всегда идет опора на базовые сведения из документов.

Для измерений применяются карты, планиметры, электронно-вычислительные машины и т.д.

Результатом проведенных работ становится максимально точно вычисленная площадь участка, однако, закон позволяет допущение незначительных погрешностей в пределах установленных норм.

В соответствии с типом земельного участка и его назначения специалисты подбирают один или несколько методов работы, которые предварительно согласуются и обсуждаются с заказчиком. Стоимость процедуры складывается из размера участка, методов его измерения и продолжительности работ. В среднем цена межевания варьируется от 10 000 рублей до 30 000 рублей.

Cпособы определения площадей в геодезии

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте). Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам — высотам и основаниям.

а, б

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).

Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l₁ и l₂, углу β₂, заключенному между ними, по формуле

Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 — 2 — 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l_1-3, используя теорему косинусов

Площадь треугольника 1 — 3 — 4 может быть вычислена по формуле

где S — полупериметр, равный

Общая площадь четырехугольника будет равна:

Источник

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны. Определение ромба звучит точно также, поэтому мы их объединили и расскажем про общие формулы расчета площади фигуры.

1. S = a * h, где a — сторона, h — высота.

2. S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето — прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.

Источник

➤

Азимуты и дирекционный угол. Магнитное склонение, сближение меридианов и поправка направления

Истинный азимут (Аи) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением истинного меридиана данной точки и направлением на объект (см. рис. 7).

Магнитный азимут (Ам) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0е до 360° между северным направлением магнитного меридиана данной точки и направлением на объект.

Дирекционный угол (α; ДУ) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением вертикальной линии координатной сетки данной точки и направлением на объект.

Магнитное склонение (δ; Ск) — угол между северным направлением истинного и магнитного меридианов в данной точке.

Если магнитная стрелка отклоняется от истинного меридиана к востоку, то склонение восточное (учитывается со знаком +), при отклонении магнитной стрелки к западу — западное (учитывается со знаком -).

Рис. 7. Углы, направления и их взаимосвязь на карте

Сближение меридианов (γ; Сб) — угол между северным направлением истинного меридиана и вертикальной линией координатной сетки в данной точке. При отклонении линии сетки к востоку – сближение меридиана восточное (учитывается со знаком +), при отклонении линии сетки к западу — западное (учитывается со знаком -).

Поправка направления (ПН) — угол между северным направлением вертикальной линии координатной сетки и направлением магнитного меридиана. Она равна алгебраической разности магнитного склонения и сближения меридианов:

Допустимая погрешность определения площади земельного участка сх назначения

Результат контроля подшивается в общую папку с межевым делом. Что такое погрешность при определении границ Межевание – это обязательная процедура для всех владельцев участков, которые хотят оформить надел во владение. Благодаря этой процедуре владелец знает, где должны быть расположены стороны его участка, а также все данные заносятся в соответствующий план.

Только после того, как эта процедура будет пройдена, можно вместе с межевым планом обратиться в кадастровую палату для постановки земли на учёт. Межевание земельных участков относится к важнейшим процедурам, необходимым для установления или подтверждения права собственности на землю с целью дальнейшего распоряжения ею.

Специфика процедуры (геодезические инструменты, сложный рельеф местности и пр.) приводит к возникновению погрешности, допустимой по закону. Для села, города, промышленной зоны и т.д. Государственные земли разграничиваются по решению федеральных властей и могут иметь в своём составе любые категории земель, и максимальное расхождение документально подтверждённых границ таких земель с рассчитанными при кадастровых работах определяется согласно таблице выше.

При расчёте погрешностей государственных земель любой категории, относящихся к особо ценным землям, а также землям заповедников (кроме водного фонда), максимальное среднеквадратичное отклонение составляет 2,5 метра.

Основные способы

Существует три основных способа определения площадей:

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

• Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
• i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

• a и b – основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

a,b,c,d – величины сторон.

Тогда площадь участка Sу будет равна:

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади

1. Площадь фигуры.

2. Способы измерения площади фигуры.

3. Равновеликие и равносоставленные фигуры.

4. Единицы площади. Отношения между ними.

5. Измерение площадей простейших фигур.

6. Измерение площадей фигур в начальной школе.

Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.

Дадим аксиоматическое определение площади, согласно и аксиоматическим определениям темы 1.

Функцией площади называется любая функция S : U R_>0, обладающая свойствами:

1) конечной аддитивности, т.е. » u, v Є u,

2) Gs — инвариантности, т.е. «u Є U, » g Є (L₂ х R 2 ),

Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно.

Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.

Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:

1) квадраты, целиком состоящие из внутренних точек фигуры Ф;

2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);

3) квадраты, не содержащие внутренних точек фигуры Ф.

покрывающей

Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.

Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m₁ и n₁ соответственно. Здесь m₁ — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n₁ — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m₁ и n₁ будут приближенными значениями измеряемой площади: первое m₁ — с недостатком; второе n₁ — с избытком.

Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m₂ и n₂ число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа

Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа

Кроме того, для любого j > 1 имеем:

Из соотношения

Допустимая погрешность при межевании земельных участков

Погрешность определения границ равна наибольшей из погрешностей при определении характерных точек. Показатели допустимой погрешности при межевании земельного участка Какая погрешность допускается при межевании? Их показатели определяет Приказ Министерства экономического развития N 518 от 17 августа 2012 года. Погрешность должна быть не более:

• 0,1 метра для земель населённых пунктов;
• 0,2 метра для сельскохозяйственных земель категорий ИЖС, ЛПХ, садоводства и огородничества;
• 0,25 метра для сельскохозяйственных земель остальных категорий и для особо охраняемых объектов, а также для земель, целевое значение которых не указано в это списке;
• 0,5 метров для водного и лесного фонда, земель запасов и специального назначения.

Таковы допустимые погрешности при межевании. Иногда земля переводится в другую категорию.

Определение азимутов и дирекционных углов

Азимуты и дирекционные углы. Положение какого-либо объекта на местности чаще всего определяют и указывают в полярных координатах, то есть углом между начальным (заданным) направлением и направлением на объект и расстоянием до объекта. В качестве начального выбирают направление географического (геодезического, астрономического) меридиана, магнитного меридиана или вертикальной линии координатной сетки карты. За начальное может быть принято и направление на какой-нибудь удаленный ориентир. В зависимости от того, какое направление принято за начальное, различают географический (геодезический, астрономический) азимут А, магнитный азимут Ам, дирекционный угол a (альфа) и угол положения 0.

Географический (геодезический, астрономический) — это двугранный угол между плоскостью  меридиана данной точки и вертикальной плоскостью, проходящей в данном направлении, отсчитываемый от направления на север по ходу часовой стрелки (геодезический азимут представляет собой двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью, проходящей через нормаль к ней и содержащей данное направление. Двугранный угол между плоскостью астрономического  меридиана данной точки и вертикальной плоскостью, проходящей в данном направлении,  называется астрономическим азимутом).

Магнитный азимут А 4м  — горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки.

Дирекционный угол а — это угол между проходящим через данную точку направлением и линией, параллельной оси абсцисс, отсчитываемый от северного направления оси абсцисс по ходу часовой стрелки.

Все вышеперечисленные углы могут иметь значения от 0 до 360 .

Угол положения 0 измеряют в обе стороны от направления, принятого за начальное. Прежде чем назвать угол положения объекта (цели),  указывают, в какую сторону (вправо, влево) от начального направления он измерен.

Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади

1. Площадь фигуры.

2. Способы измерения площади фигуры.

3. Равновеликие и равносоставленные фигуры.

4. Единицы площади. Отношения между ними.

5. Измерение площадей простейших фигур.

6. Измерение площадей фигур в начальной школе.

Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.

Дадим аксиоматическое определение площади, согласно и аксиоматическим определениям темы 1.

Функцией площади называется любая функция S : U R_>0, обладающая свойствами:

1) конечной аддитивности, т.е. » u, v Є u,

2) Gs — инвариантности, т.е. «u Є U, » g Є (L₂ х R 2 ),

Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно.

Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.

Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:

1) квадраты, целиком состоящие из внутренних точек фигуры Ф;

2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);

3) квадраты, не содержащие внутренних точек фигуры Ф.

покрывающей

Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.

Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m₁ и n₁ соответственно. Здесь m₁ — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n₁ — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m₁ и n₁ будут приближенными значениями измеряемой площади: первое m₁ — с недостатком; второе n₁ — с избытком.

Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m₂ и n₂ число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа

Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа

Кроме того, для любого j > 1 имеем:

Из соотношения

Число s называют значением внутренней площади фигуры Ф, а число S — значением внешней площади. Очевидно, что s £ S, т.к. при любом номере i имеет место неравенство m_i £ n_i.

1.2. Измерение по карте прямых и извилистых линий

Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.

Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 2); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).

Рис. 2. Определить по карте расстояние между точками местности с помощью линейки.

Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 3). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.

Рис. 3. Измерение на карте расстояний циркулем-измерителем по линейному масштабу

Рис. 4. Измерение на карте расстояний циркулем-измерителем по извилистым линиям

Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.

В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 2).

Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.

Таким же способом измеряют расстояния по извилистым линиям (рис. 4). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.

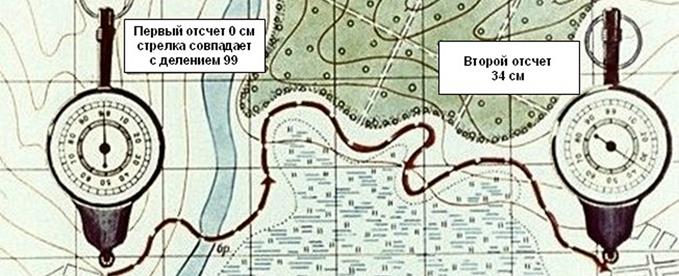Рис. 5. Измерения расстояния курвиметром

Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 5), который особенно удобен для измерения извилистых и длинных линий.

В приборе имеется колесико, которое соединено системой передач со стрелкой.

При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)

Сближение меридианов. Переход от геодезического азимута к дирекционному углу.

Сближение меридианов y — это угол в данной точке между ее меридианом и линией, параллельной оси абсцисс или осевому меридиану.

Направлению геодезического меридиана на топографической карте соответствуют боковые стороны ее рамки, а также прямые линии, которые можно провести между одноименными минутными делениями долгот.

Счет сближения меридианов ведется от геодезического меридиана. Сближение меридианов считается положительным, если северное направление оси абсцисс отклонено к востоку от геодезического меридиана и отрицательным, если это направление отклонено к западу.

Величина сближения меридианов, указанная на топографической карте в левом нижнем углу, относится к центру листа карты.

При необходимости величину сближения меридианов можно вычислить по формуле

y=(L — L 4) sin B,

где L — долгота данной точки;

L 4— долгота осевого меридиана зоны, в которой расположена точка;

B — широта данной точки.

Широту и долготу точки определяют по карте с точностью до 30`, а долготу осевого меридиана зоны рассчитывают по формуле

L 4= 4  06 5  0N — 3 5,

где N — номер зоны

Пример. Определить сближение меридианов для точки с координатами:

B = 67 5о 040` и L = 31 5о 012`

31 5о 012`

Решение. Номер зоны     N = ______ + 1 = 6;

6 5о

L 4o  0= 4  06 5о 0 * 6 — 3 5о 0 = 33 5о 0;  y = (31 5о 012` — 33 5о 0) sin 67 5о 040` =

-1 5о 048` * 0,9245 = -1 5о 040`.

Сближение меридианов равно нулю, если точка находится на осевом меридиане зоны или на экваторе. Для любой точки в пределах одной координатной шестиградусной зоны сближение меридианов по абсолютной величине не превышает 3 5о 0.

Геодезический азимут направления отличается от дирекционного угла на величину сближения меридианов. Зависимость между ними может быть выражена формулой

A = a + (+ y)

Из формулы легко найти выражение для определения дирекционного угла по известным значениям геодезического азимута и сближения меридианов:

a = А — (+ y).

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность – это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

• mt – СКП расположения поворотных точек;
• P – площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.

Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.